Méthode de décomposition de domaines pour le calcul du tenseur élastique homogénéisé de matériaux aléatoires
Research team: Virginie Ehrlacher (CERMICS), Éric Cancès (CERMICS), Frédéric Legoll (NAVIER)
June 2017 – May 2018
The aim of this project was to develop an efficient and original numerical method in order to compute the effective properties of random materials. In particular, we focused on heterogeneous materials containing inclusions embedded in a matrix, where the typical scale of the inclusions is small with respect to the size of the domain occupied by the material. These inclusions are supposed to be randomly distributed in the material.
In this case, the effective properties of the material are deterministic, and their computation by a full-field method requires the resolution of an auxiliary problem defined over the entire space. Classical methods consist in considering a large (but finite) statistical elementary volume, on which the auxiliary problem is solved using appropriate (e.g. periodic) boundary conditions. The size of the elementary volume should be sufficiently large to represent accurately the statistical properties of the distribution of the inclusions in the material. However, of course, the larger this size, the more expensive the computations are.
In this project, we have considered another type of auxiliary problem, defined over the whole space, where the statistical elementary volume is embedded in an exterior infinite homogeneous material. The new problem can then be seen as a generalization of the Eshelby problem. The interest of considering such an alternative formulation lies in the fact that a very efficient numerical method, based on domain decomposition methods and an integral formulation of the equations, can be used to solve these problems.
In the first part of the project, we have focused on a thermal problem. A typical numerical example is as follows. We consider a 3D random material, with polydisperse spherical inclusions. The radii of the spheres are uniformly distributed between 0.1 and 0.25, their centers are uniformly distributed (under the constraint of no interpenetration), and the diffusion coefficient in each sphere is uniformly distributed between 10 and 50. We consider a sphere of radius R (with R between 2 and 20), which contains the heterogeneous material. Beyond this sphere, the material is supposed to be homogeneous, with a well-chosen diffusion coefficient. The largest configuration thus consists of 32442 inclusions.
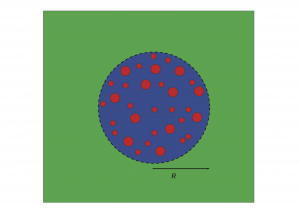
From the solution of the embedded corrector problem, we have been able to compute accurate approximation of the homogenized matrix, with a limited computational cost.
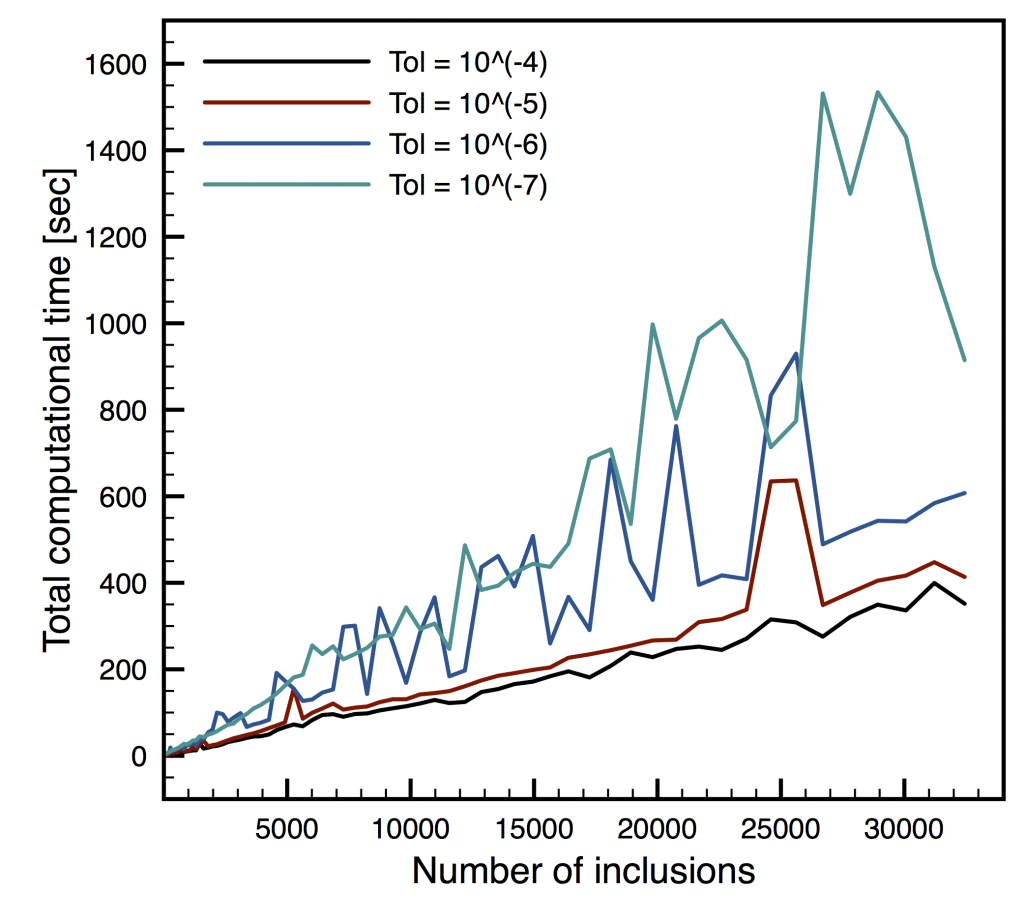
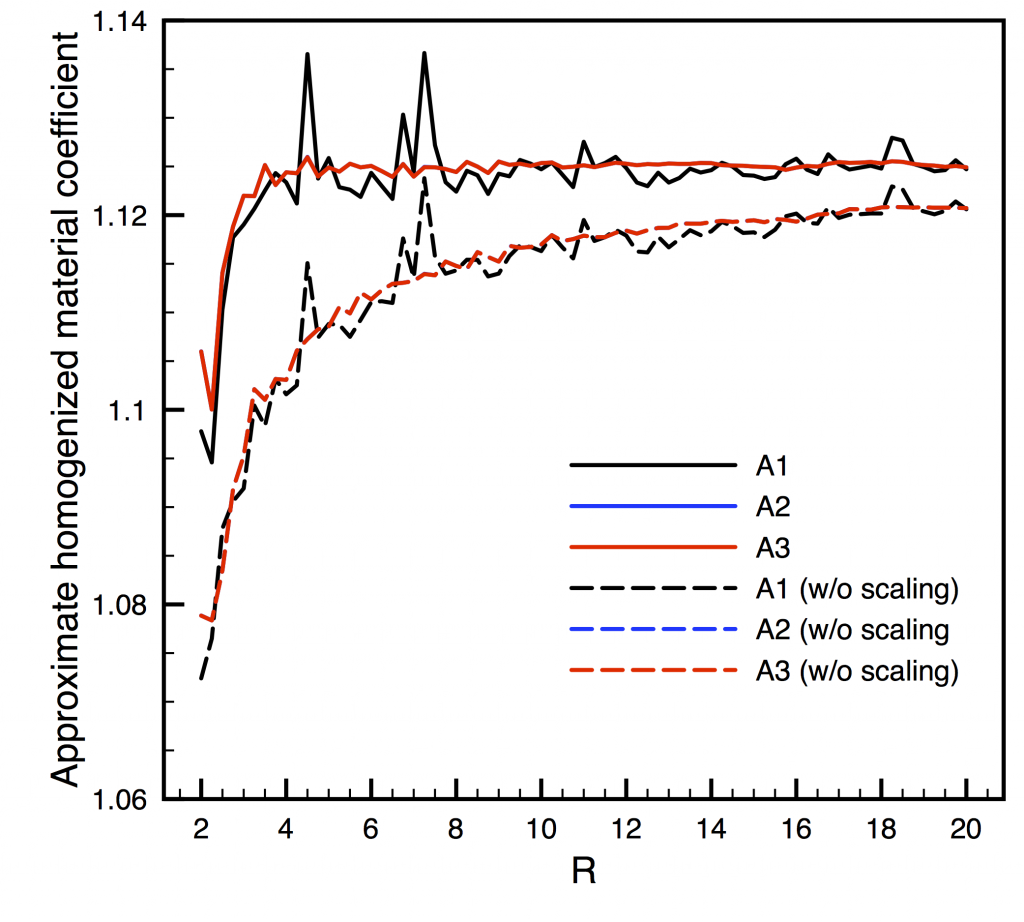
We have next turned to the elasticity case. We have been able to extend the theoretical approach. We have also been able to extend the numerical implementation, by developping vectorial spherical harmonics (that play the role of spherical harmonics for scalar problems) that allow us to obtain accurate results for an affordable computational cost.
Publications:
[1] Cances, E., Ehrlacher, V., Legoll, F., Stamm, B., and Xiang, S., An embedded corrector problem for homogenization. Part I: Theory. HAL preprint 01840993.
[2] Cances, E., Ehrlacher, V., Legoll, F., Stamm, B., and Xiang, S., An embedded corrector problem for homogenization. Part II: Algorithms and discretization.
arxiv preprint 1810.09885 and HAL preprint 01903486
