The computation of homogenized coefficients through a full-field approach is often very expensive. These coefficients are indeed defined from the solution of a local problem, posed on a domain (the so-called RVE) which should be as large as possible. In addition, since the RVE is finite, only a random approximation of the exact deterministic coefficients can be computed.
To circumvent this difficulty, many reduced models have been proposed in the literature: selfconsistent models, Hashin-Shtrikman bounds, Mori-Tanaka like schemes, … These schemes (which are based on analytical formulaes) typically make use of a small number of statistical informations on the microstructure (for composite materials, the volume fractions, the shape and orientation of the inclusions, …) and provide an approximation of the homogenized quantities.
The purpose of the postdoc was to use these reduced models not to compute the final result, but in a control variate approach, which can be seen as a predictor-corrector approach: the reduced model is used to predict a result, which is next corrected using the reference model. The computational cost is hence similar to standard Monte-Carlo approaches (one still need to solve the corrector problem on large domains), but the accuracy is significantly improved.
During the postdoc of Michael Bertin, we have constructed a reduced model, derived from the Hashin-Shtrikman variational principle, and the computation of which is inexpensive in comparison to full-field computations. We have next comprehensively tested the variance reduction approach on a composite made of circular inclusions randomly located in a matrix (see Figure on the left below). The reduced model not only depends on the volume fraction of inclusions, but also on higher degree microstructure descriptors. Significant gains in accuracy (at equal computational cost) have been obtained, even for very large contrasts (see Figure on the right below). The influence of other parameters (including the size of the RVE, and the minimal distance between inclusions) have also been examined.
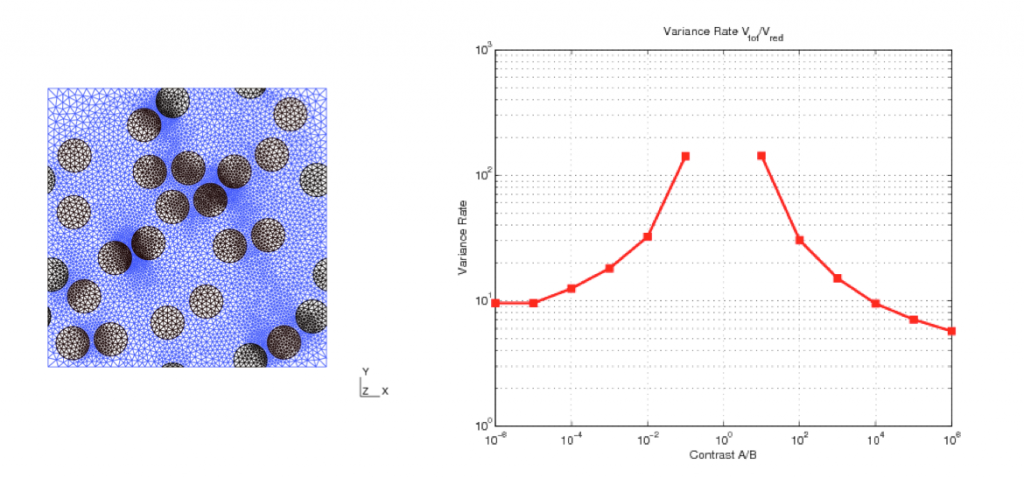
A long-term goal of this project is to better understand which characteristics of the microstructure have an impact in the fluctuations of the apparent homogenized properties. Obtaining accurate estimations of the homogenized properties is indeed often critical to determine whether or not some parameters of the microstructure (such as the minimal distance between inclusions) affect the macroscopic behavior.
The results obtained within this postdoc have already been presented in various scientific conferences. They will be the topic of an international journal article.
