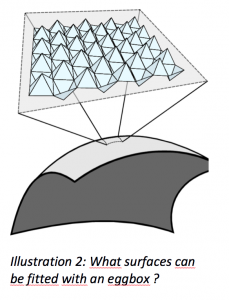
In various domains including architecture, civil engineering, aerospace engineering and biomedical engineering, structures that are compact, deployable and controllable have found interesting applications. These structures are often easily fabricated by periodically reproducing a simple unit-cell in two directions of space. Sometimes, models are obtained by periodically pleating, cutting and/or glueing a sheet of paper. In any case, it is of interest to study into what surfaces these structures deform and, conversely, what surfaces can be fitted using a given unit-cell.
To better understand the foregoing question, one can model a unit-cell as a pin-jointed truss, i.e., an assembly of rigid bars and pivots. A unit-cell becomes then a mechanism of a given number of degrees of freedom. The structure can the be seen as a periodic truss whose rigid, sometimes called floppy or zero-energy, modes are of interest. We simplify this question further by assuming that the size of a unit-cell is small compared to the size of the truss. In other words, we are only looking for smooth surfaces which can be fitted using a big number of unit-cells. Hence, an upscaling form discrete to continuum kinematics will turn out to be possible.
 To answer this question, we suggest a few formal asymptotic tools in order to justify the upscaling of the discrete truss into a continuous surface. These tools allowed to establish a connection between the first fundamental form, i.e., the metric, and the second fundamental form, i.e., the curvatures, on one hand, and the linear and quadratic rigid deformation modes of the unit-cells on the other hand. Our conclusion reads as a necessary fitting condition: given a unit-cell of size r and a smooth surface S, if S can be fitted asymptotically for, then S admits a parametrization φ satisfying a known system of partial differential equations.
To answer this question, we suggest a few formal asymptotic tools in order to justify the upscaling of the discrete truss into a continuous surface. These tools allowed to establish a connection between the first fundamental form, i.e., the metric, and the second fundamental form, i.e., the curvatures, on one hand, and the linear and quadratic rigid deformation modes of the unit-cells on the other hand. Our conclusion reads as a necessary fitting condition: given a unit-cell of size r and a smooth surface S, if S can be fitted asymptotically for, then S admits a parametrization φ satisfying a known system of partial differential equations.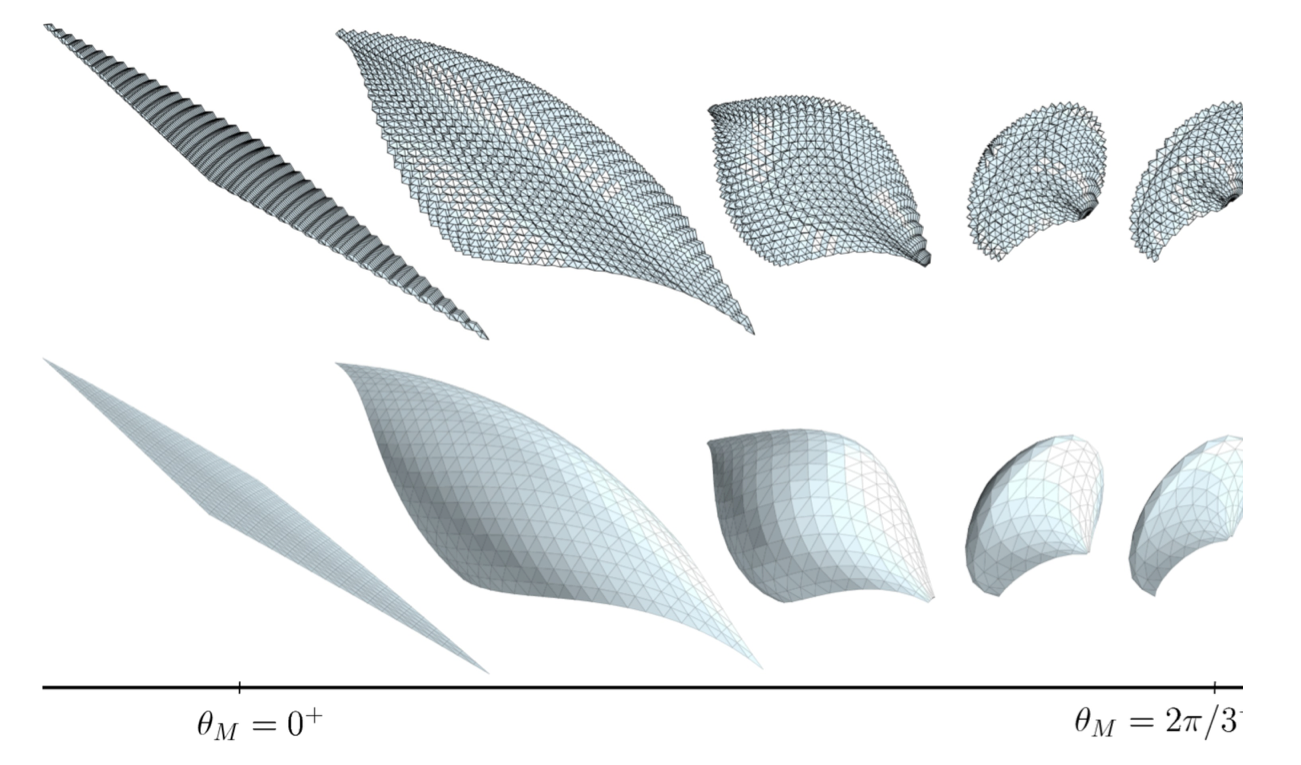
We have applied this method to the study of many structures: a pyramidal truss, the eggbox and the Miura-ori among others. The results for the Miura-ori complete those found in the literature. The results for the eggbox are new and are the core of a journal paper that will be submitted shortly (the text of said paper is enclosed to this abstract).
Last, a code was written in Python to generate and visualize in 3D the studied structures in order to assess our theoretical findings. The results were published in an article. We have also been accepted for the IASS conference in September 2017 in Hamburg, where we will submit a proceeding.
Reference:
Nassar, H., Lebée, A. and Monasse, L. (2017), Curvature, metric and parametrization of origami tessellations: Theory and application to the eggbox pattern, Proceedings of the Royal Society A, 473 : 2197, doi:10.1098/rspa.2016.0705, hal-01368009.
