A comparative study of Biot’s theory and Willis’ theory
for periodically stratified media
with alternating solid and fluid layers
The present study aims at comparing the predictions of Biot’s theory and Willis’theory with that of the exact theory in describing the dynamic behavior of a periodically stratified medium containing alternating solid and fluid layers (Fig. 1). The exact theory refers to the propagator matrix method [1] in this study which gives the exact solutions of the problem as a basis to justify the predictions of the other theories. Biot’s theory of poroelasticity [2, 3] is an efficient phenomenological tool in modeling a porous frame saturated by a fluid, however, it requires that the wavelength is relatively large compared to the size of the representative elementary volume (VER). Willis’ theory is a dynamic homogenization theory which yields the effective constitutive law exhibiting the non-classical coupling between the effective stress and effective velocity, and that between the effective momentum and effective strain [4]. Willis [5] has justified the effective constitutive law with above-mentioned coupling by studying one-dimensional wave propagation in a stratified medium containing two different solids. In this study we would like to follow the same procedure and to study the Willis’ theory in the particular case of a stratified medium containing alternating solid and fluid layers for which the exact solution is available.
 Fig. 1. A periodically stratified medium composed of alternating solid and fluid layers.
Fig. 1. A periodically stratified medium composed of alternating solid and fluid layers.
Figure 2 shows the comparison between predictions of exact theory and Biot’s theory for the case of wave propagation in a periodically stratified medium composed of elastic solid layer and ideal fluid layers. It can be seen that Biot’s theory agrees with the exact solution only in the frequency range where the response is linear. In the subsequent step, the Willis formulation will be adapted in the problem and the result will be compared with those of the exact solution and Biot’s theory. It is expected that Willis’ theory would eventually be dispensed from the limitation of Biot’s theory and lead to a effective constitutive law more representative of the exact dynamic behaviors of the medium.
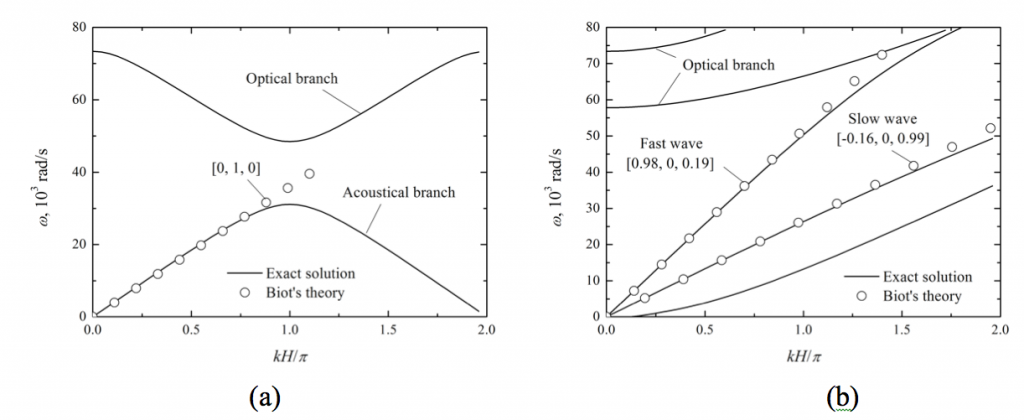 Fig. 2. Dispersion curves with different angle of incidence and comparison with Biot’s theory: (a) incidence normal to the layers and (b) incidence parallel to the layers.
Fig. 2. Dispersion curves with different angle of incidence and comparison with Biot’s theory: (a) incidence normal to the layers and (b) incidence parallel to the layers.
References
[1] Gilbert, K. E., 1983, ” A Propagator Matrix Method for Periodically Strafified Media,” Journal of the Acoustical Society of America, 73(2), 137-142.
[2] Biot, M. A., 1956, “Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. I. Low Frequency Range,” Journal of the Acoustical Society of America, 28(2), 168-178.
[3] Biot, M. A., 1956, “Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. Ii. Higher Frequency Range,” Journal of the Acoustical Society of America, 28(2), 179-191.
[4] Willis, J. R., 1997, Continuum Micromechanics, Springer-Verlag, New York, Dynamics of Composites, 265-290.
[5] Willis, J. R., 2009, “Exact Effective Relations for Dynamics of a Laminated Body,” Mechanics of Materials, 41(4), 385-393.
