Modelling cracking of heterogeneous, porous materials subjected to hydromechanical stresses by means of the joint finite element method and micromechanical models
Advisors: Amade Pouya (NAVIER), Sébastien Brisard (NAVIER)
The aim of this project is to investigate cracking of porous (clayey) geomaterials induced by mechanical or hydric loading. Two methods will be used.
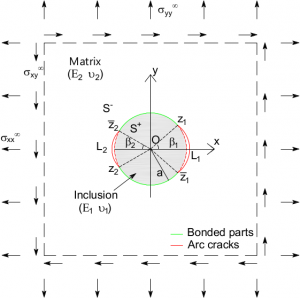
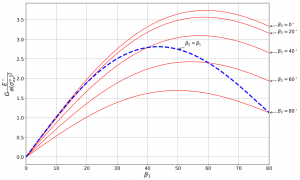
In the first approach, we will develop a micromechanical model based on the solution to Eshelby’s problem for a partially bonded inhomogeneity. The method of complex potentials of Muskhelishvili is applied to derive a semi-analytical solution to this problem in the 2D case. A subsequent energy analysis shows that two initially symmetrical interfacial cracks at the boundary of a circular inclusion might propagate asymmetrically. This fundamental solution is the building block of classical micromechanical methods that will be used to derive a macroscopic damage model.
- The fundamental problem of a single inclusion, embedded in an infinite matrix to which it is partially bonded
- An energy analysis shows that asymmetrical propagation of cracks may be more favorable even for symmetric geometries and loading conditions
In the second approach, full-field simulations will be carried out by means of the finite element method. Cracking will be modelled through joint elements and a cohesive zone model.
The study will then be extended to porous materials subjected to hydromechanical loadings
Publications:
Articles in peer-reviewed journals:
- Le V.H.T., Brisard S., Pouya A., (2019), Debonding of a circular inclusion: Asymmetric propagation of a pair of cracks, International Journal of Solids and Structures, 167, 71-78 (DOI:10.1016/j.ijsolstr.2019.03.004)
Conference papers:
- Le V.H.T., Brisard S., Pouya A., (2018), Elastostatic problem of two asymmetrical cracks along the inclusion-matrix interface under a remote uniform load, 41st Solid Mechanics Conference, August 2018, Warsaw, Poland