Initiation of mechanical failure
Research team: L. Brochard, F. Legoll and K. Sab (Navier), E. Cances, T. Lelièvre and G. Stoltz (CERMICS)
PhD project started October 2015, defended September 30, 2018
The Ph.D. project of Sabri Souguir is dedicated to the study of the physics of failure initiation in brittle materials, for which there is no scientific consensus yet. The objective of the Ph.D. project is the study of initiation at the atomic scale with molecular simulation tools in order to unravel the physical mechanisms of failure and ultimately develop or identify an analytical criterion that can be used at the engineering scale.
A preliminary series of simulations of a 2D graphene-like material were performed in the context of a previous labex project (postdoc of Ignacio Tejada). This series of simulations has shown that 1) it is possible to capture the initiation phenomenon at scales accessible to molecular simulations, provided that the materials considered are sufficiently brittle; 2) locally, a material can significantly overcome the strength limit of the bulk; 3) Very few existing initiation models are consistent with the failure behavior of this example. Only one model (Leguillon’s criterion) seems to provide a reasonable interpretation and good quantitative predictions. A specificity of this model is that it allows stresses exceeding strength in peculiar situations for which the mechanical energy that can be released by failure is lower than the energy release rate of the material.
This preliminary study raises many questions that motivated the Ph.D. project:
- What physical mechanisms are at the origin and failure that can explain the transition from energy to stress criteria macroscopically?
- Is there a general theoretical framework that can encompass all situations of failure?
- Can such a general theory be used to propose or support a universal criterion for failure initiation at the macroscopic scale?
In order to answer these questions, we started a systematic study of a realistic representation of graphene accounting for the third dimension and making use of up-to-date inter-atomic potentials. In parallel, we also started a systematic study of a toy model made of atoms on a 2D triangular lattice interacting with simple harmonic springs. The graphene simulations aim at assessing the failure behavior of a more realistic case than that considered in the preliminary study. Whereas the toy model study offers the possibility to easily confront the theory since many analytical analysis are made possible on such simple systems.
Two essential results have been obtained in this work, which reshape our vision of failure initiation:
- We found that strength and toughness exhibit similar scaling with temperature and loading rate but differ regarding system size. The scaling law can be theoretically understood by considering failure as a thermally activated process: failure corresponds to the occurrence of a transition state that requires the overcome of an energy barrier. Thus, the failure stress depends on thermal agitation (temperature), loading rate and the number of possible failure transitions available in the phase space (~system size for strength and number of cracks for toughness). Interestingly, this finding proves that strength and toughness originate from similar physical mechanisms, the only difference being that stress concentration for fracture failure strongly limits the number of accessible transition states to the vicinity of the flaws. This work is the first to propose a generalized scaling law in temperature, loading rate and system size for both strength and toughness. Such time-size-temperature equivalence is of intrinsic interest for any confrontation between highly different length and time scales such as comparing molecular simulation results and laboratory experiments.
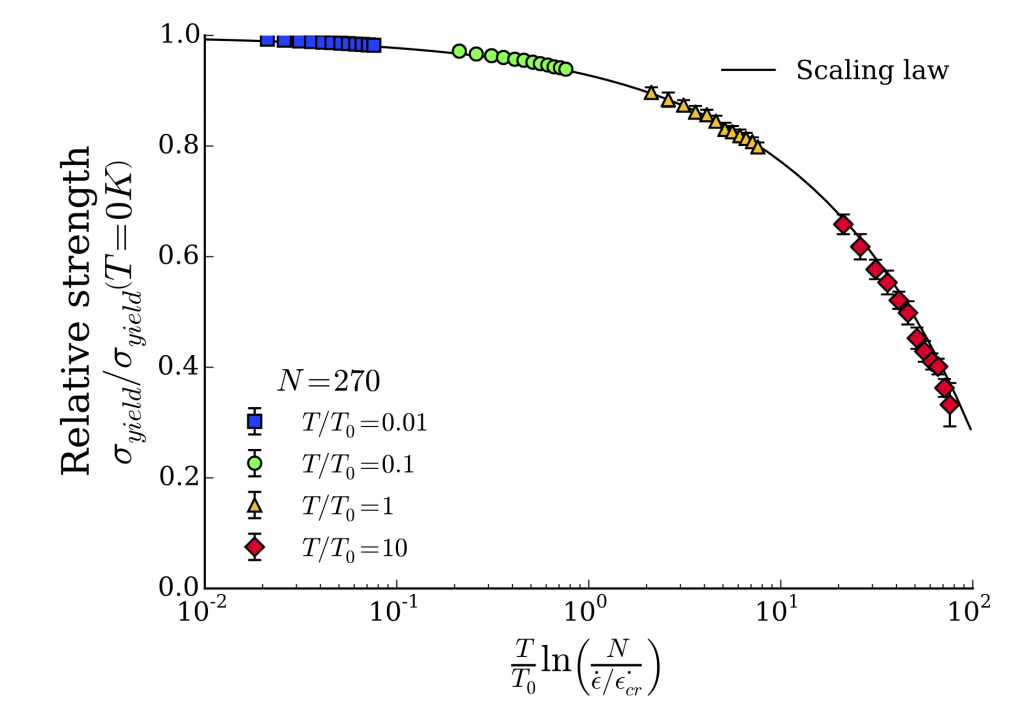
Scaling of strength
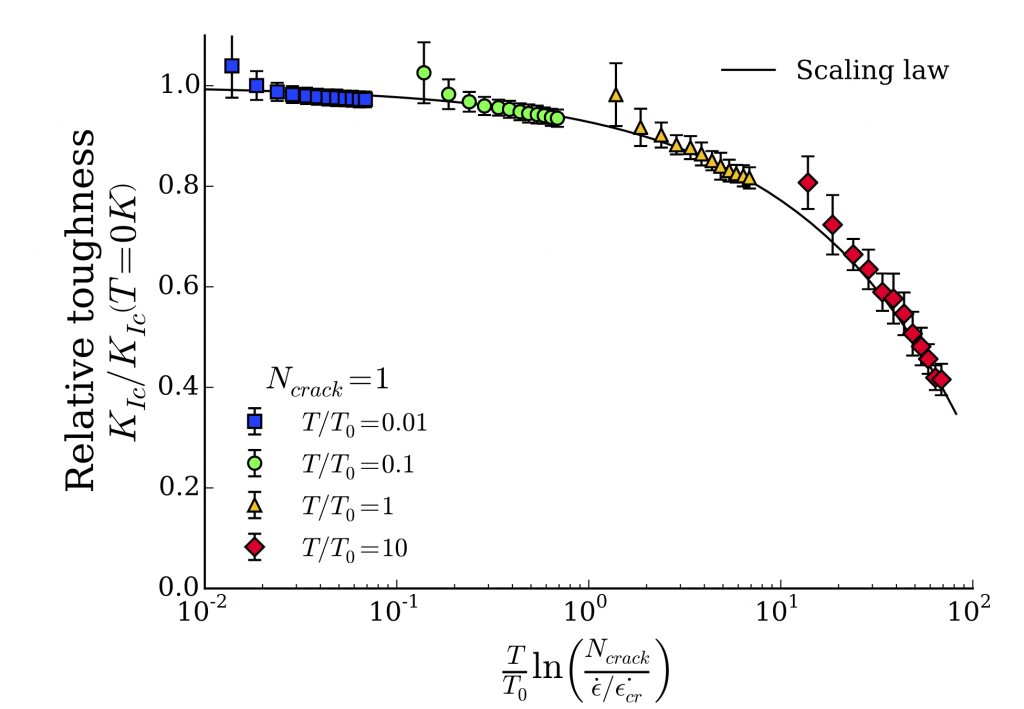
Scaling of toughnes
- With the generalized scaling law, one is left with understanding the problem of failure initiation at 0K only, which is a significant simplification. Failure at 0K can be treated as an instability problem. Indeed, since the inter-atomic force field is a multivariate infinitely derivable function of the atomic positions, 0K failure corresponds precisely to the occurrence of a negative eigenvalue of the Hessian matrix of the system (matrix of the second derivatives of the potential with respect to the atomic positions). The associated eigenvector describes the combined atom displacements that give rise to energy release by failure. In the absence of stress concentration, the eigenvectors show that atom must separate over long initiation bands, whereas with stress concentration, the eigenvectors are much more localized. Interestingly, the initiation bands for homogenous systems have a thickness that corresponds to the characteristic length given by the ratio between toughness and strength. The origin of this characteristic length, also known as process zone, is a long-standing issue in mechanics. In this work we show that this length can be identified by the study of an intact body only (whereas toughness characterizes the failure of cracked bodies). And its interpretation is the size over which collective movement of atoms are required to start the failure at the transition state. Interestingly, the degeneracy of the smallest eigenvalue scales as a power of the number of atoms for pristine materials, but as the number of cracks (all identical) for flawed materials. This degeneracy quantifies the number of transition paths to failure, and thus explains the difference of scaling with size between strength and toughness at finite temperature.
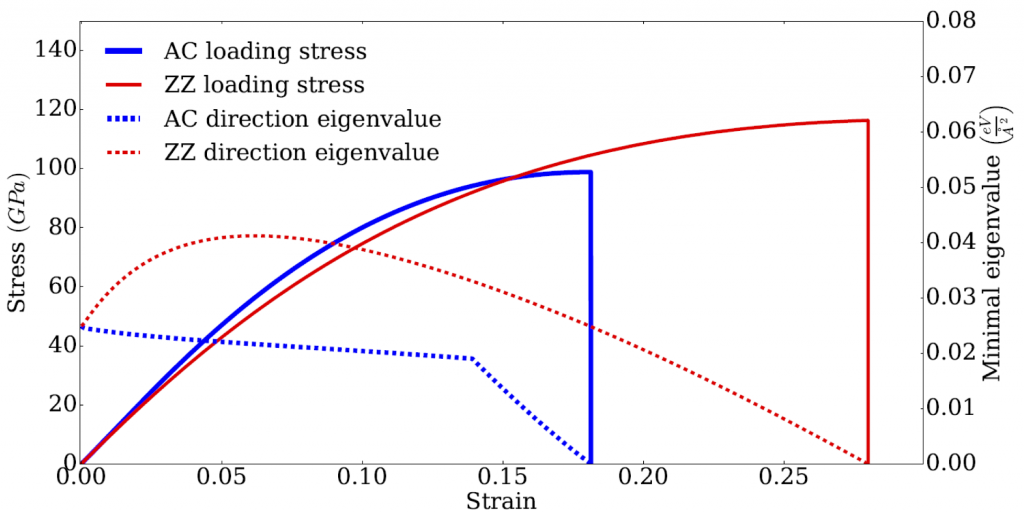
Evolution of the smallest eigenvalue of the Hessian during the loading of graphene

Eigenvector of the smallest eigenvalue at failure describing the mechanism of failure in ZigZag
Publications:
[1] Brochard, L., Souguir, S., & Sab, K. (2018). Scaling of brittle failure: strength versus toughness. International Journal of Fracture, 210(1-2), 153–166, doi:10.1007/s10704-018-0268-9, hal-01744161
[2] Souguir, S., Brochard, L., & Sab, K. (2020) Stress concentration and instabilities in the atomistic process of brittle failure initiation. International Journal of Fracture, 224(2), 235–249, doi:10.1007/s10704-020-00459-x
