The purpose of the PhD thesis of William Minvielle is to design numerical techniques to address the homogenization of equations, the coefficients of which exhibit small scale random heterogeneities. Such equations are often used to model heterogeneous media (composite materials, concrete, subsurface media, …). Solving such partial differential equations is prohibitively expensive due to the discrepancy of scales between the characteristic size of the heterogeneities and the size of the macroscopic domain that is to be considered.
One may use homogenization theory to reduce the complexity of this task and substitute the random, fine scale oscillating coefficients of the equation with constant, deterministic homogenized coefficients. These coefficients are defined using an ergodic average, which is challenging to compute in practice. The thesis introduces, studies and compares variance reduction methods (antithetic variables, control variate, quasi random structures) useful for the Monte-Carlo approximation of these coefficients. Significant variance reduction ratios have been obtained for each of the proposed methods.
We now briefly review each work composing this thesis.
The first work that has been performed consists in investigating how to use the technique of antithetic variables to obtain a better approximation of the apparent properties (that is, estimates with a smaller confidence interval, namely less statistical noise, at equal computational costs). Such a technique is widely used in other fields of applications. It is a generic technique which consists in generating, together with each random realization of the material, another realization (a so-called antithetic realization), which is somehow a mirror of the former. The technique is easy to implement, and provides interesting gains in efficiency in comparison to a standard Monte Carlo approach. In some previous works, not funded by the Labex MMCD, we have explored this technique for materials described by a linear constitutive law. Within the thesis of W. Minvielle, we have extended the approach to nonlinear materials (think e.g. of finite deformation elasticity). We have observed that the nonlinearity does not affect the efficiency of the approach. Computational gains are similar for either linear or nonlinear materials.
The antithetic variable technique is very generic and does not exploit much of the specificities of the problem. The subsequent works that we have performed exploit much more the structure of the random homogenization problems. They lead to much larger computational gains.
We have next proposed a variance reduction procedure, based on the control variate technique, to again obtain estimates of the apparent homogenized tensor with a smaller statistical error than standard Monte Carlo approaches. The control variate technique is based on using a surrogate model, somewhat in the spirit of a preconditionner. This surrogate model should be simple enough such that the mean (over all realizations of the microstructure) of its response should be computable, and close enough to the reference model such that its fluctuations look alike those of the reference model. The idea of the control variate technique is essentially to subtract the fluctuations of the surrogate model from those of the reference model. In the control variate approach, the reduced model is problem dependent: the better it is, the larger the computational gain. The surrogate model that we have used here is inspired by a weakly stochastic approach previously introduced by A. Anantharaman and C. Le Bris to describe periodic models perturbed by rare defects. This reduced model provides an accurate description of the material in the case when defects are indeed rare. We have used that reduced model in the regime when defects are not rare (see Figure on the left below). As such, it is thus not accurate (and it is not meant to be), but it provides enough information on the reference model to allow for an overall improvement in full-field computations of the homogenized properties (see Figure on the right below).
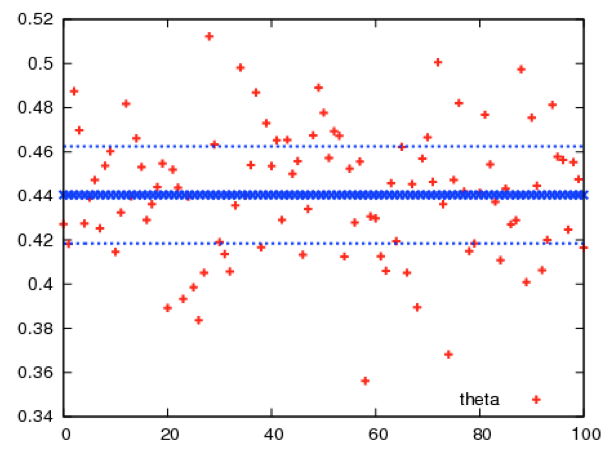
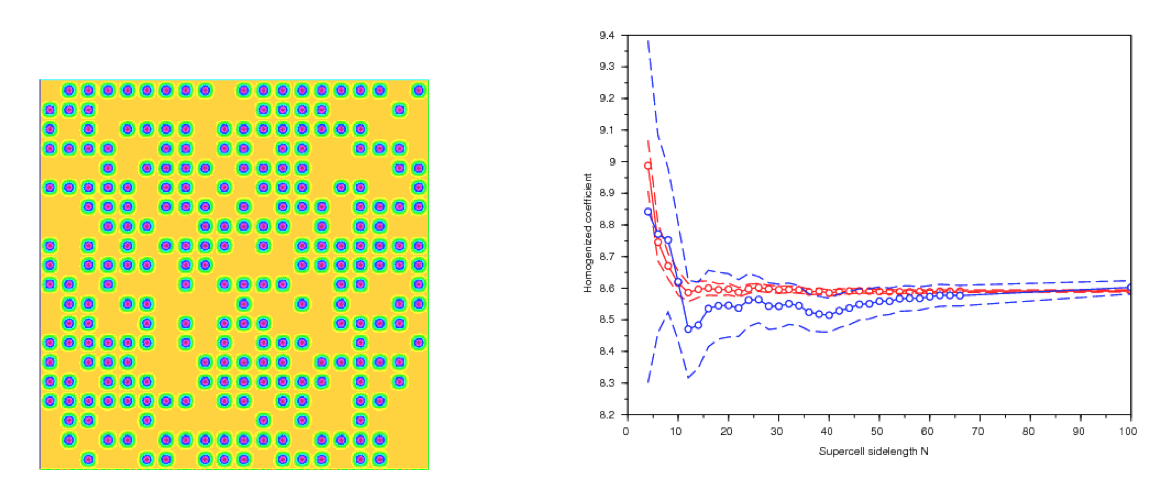 The third topic that has been investigated concerns the possibility to use a technique based on computing the corrector equation only for selected environments. These environments are chosen based on the fact that their statistics in the finite supercell matches the statistics of the materials in the infinite supercell. A first approach is to consider microstructures such that the apparent volumic fraction in the supercell is equal to the asymptotic value. A variant consists in generating many microstructures, and only retaining the small proportion of those for which the apparent volumic fraction is close to the asymptotic value (see Figure below). Of course, higher order descriptors, beyond the volumic fraction, may (and have been) used. In that technique, we thus a priori select the good environments (i.e. microstructures). The apparent homogenized properties are only computed for these selected environments.
The third topic that has been investigated concerns the possibility to use a technique based on computing the corrector equation only for selected environments. These environments are chosen based on the fact that their statistics in the finite supercell matches the statistics of the materials in the infinite supercell. A first approach is to consider microstructures such that the apparent volumic fraction in the supercell is equal to the asymptotic value. A variant consists in generating many microstructures, and only retaining the small proportion of those for which the apparent volumic fraction is close to the asymptotic value (see Figure below). Of course, higher order descriptors, beyond the volumic fraction, may (and have been) used. In that technique, we thus a priori select the good environments (i.e. microstructures). The apparent homogenized properties are only computed for these selected environments.
This method yields an approximation of the homogenized matrix with a smaller error that standard approximations. We have demonstrated the efficiency of the approach for various types of random materials (see Figure below), including composite materials with randomly located inclusions.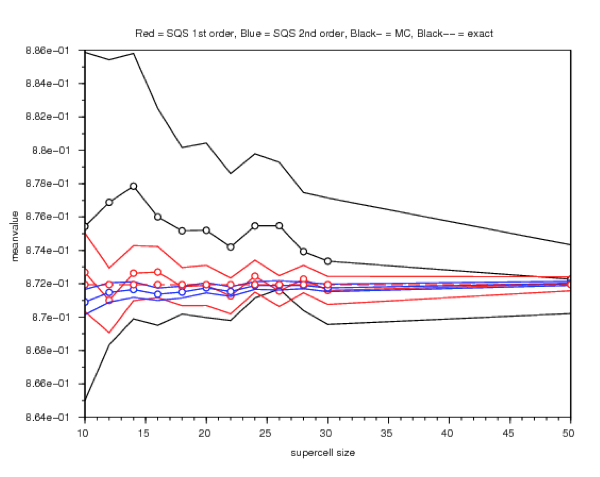
Publications:
Le Bris, C., Legoll, F., and Minvielle, W., (2016), Special Quasirandom Structures: a selection approach for stochastic homogenization, Monte Carlo Methods and Applications, 22 (1), 25-54. (HAL preprint 01194480).
Legoll, F., and Minvielle, W., (2015), A control variate approach based on a defect-type theory for variance reduction in stochastic homogenization, SIAM Multiscale Modeling and Simulation, 13 (2), 519-550 (HAL preprint 01053459).
Legoll, F., Minvielle, W., Obliger, A. and Simon, M., (2015), A parameter identification problem in stochastic homogenization, ESAIM Proceedings, 48, 190-214 (HAL preprint 00942730).
Legoll, F., and Minvielle, W., (2015), Variance reduction using antithetic variables for a nonlinear convex stochastic homogenization problem, Discrete and Continuous Dynamical Systems – S, 8 (1), 1-27 (HAL preprint 00784187).
