Modeling of random heteregeneous materials: from microscale to macroscale
Keywords: Homogenization, Probabilistic modeling, Micromechanics, Gradient materials.
If the length-scales are well separated, homogenization theory can provide a robust theoretical framework for heterogeneous materials. In this context, the macroscopic properties can be retrieved from the solution to an auxiliary problem, formulated over the representative volume element (with appropriate boundary conditions). This two-part PhD work by V.P. Tran is focused on the homogenization of heterogeneous materials. They are described at the finest scale by two different material models (both depending on a specific characteristic length) while the homogeneous (macroscopic) medium behaves as a classical Cauchy medium in both cases.
Stochastic modeling of mesoscopic elasticity random field (Tran et al., 2016)

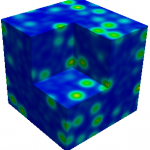 In the first part of this PhD work, the random microstructure of a Cauchy medium is considered. Solving the auxiliary problem on multiple realizations can be very costly due to constitutive phases exhibiting not well-separated characteristic length scales and/or high mechanical contrasts (see figure on the left). In order to circumvent these limitations, our study is based on a mesoscopic description of the material, combined with information theory. In the mesostructure, defined by a filtering framework, the fine-scale features are smoothed out (see figure on the right).
In the first part of this PhD work, the random microstructure of a Cauchy medium is considered. Solving the auxiliary problem on multiple realizations can be very costly due to constitutive phases exhibiting not well-separated characteristic length scales and/or high mechanical contrasts (see figure on the left). In order to circumvent these limitations, our study is based on a mesoscopic description of the material, combined with information theory. In the mesostructure, defined by a filtering framework, the fine-scale features are smoothed out (see figure on the right).
The mesostructure is a (tensorial) random field, which is characterized statistically. A model for this random field is then proposed and suitably calibrated. It allows to generate realizations of the mesostructure without prior generation and simulation of fully resolved microstructures. The model is shown to deliver very accurate estimates of the macroscopic properties, while significantly reducing the computational cost.
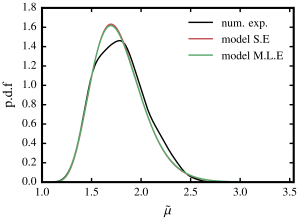
Probability distribution function of the filtered shear modulus of the true and model mesostructures.
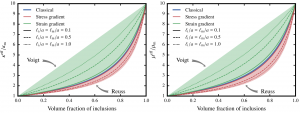
Mori–Tanaka estimates of the effective bulk (left) and shear (right) moduli of the composite, as a function of the volume fraction of inclusions. The estimates are represented for both stress- and strain-gradient materials.
Mori-Tanaka estimates of the effective elastic properties of stress-gradient composites (Tran et al., 2018)
The second part of this PhD work is dedicated to gradient materials which induce microscopic size-effect due to the existence of microscopic material internal length(s). The random microstructure is described by a newly introduced stress-gradient model. Despite being conceptually similar, we show that the stress-gradient and strain-gradient models define two different classes of materials. Next, simple approaches such as mean-field homogenization techniques are proposed to better understand the assumptions underlying the stress-gradient model. The obtained semi-analytical results allow us to explore the influence on the homogenized properties of the model parameters and constitute a first step toward full-field simulations.
Publications
Tran, V.P., Brisard, S., Guilleminot, J., Sab, K. (2018), Mori-Tanaka estimates of the effective elastic properties of stress-gradient composites, International Journal of Solids and Structures, 146, 55-68. hal-01740741
Tran, V.P., Guilleminot, J., Brisard, S., Sab, K., (2016), Stochastic modeling of mesoscopic elasticity random field, Mechanics of Materials, 93, 1-12, hal-01226337
Tran, V.P., Guilleminot, J., Brisard, S., Sab, K., (2015), Homogénéisation numérique à l’aide de modèles prior de la raideur mésoscopique : identification et validation, 22ème Congrès Français de Mécanique, Lyon, France, hal-01194370
