The contact between rough surfaces is a phenomenon met in various situations [1]. In general, the quantitative study of this phenomenon necessitates numerical approaches. The present PhD thesis work deals with the computational analysis of the problem of unilateral contact between a rigid half-space with a periodically wavy surface and a deformable half-space with a smooth surface. Small deformations and frictionless condition are considered. In this case, the contact area, the contact pressure distribution and the vertical displacement of the smooth surface are periodic (Figure 1).
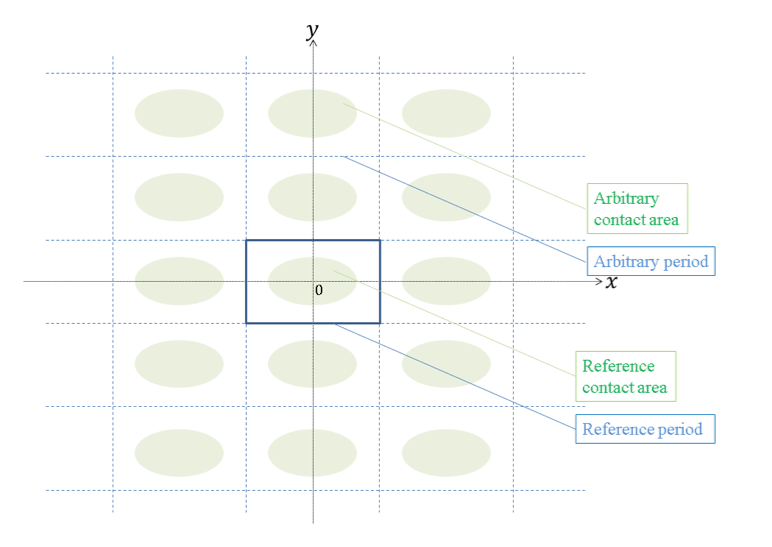 Figure 1: contact between a rigid periodically wavy surface and a deformable half-space.
Figure 1: contact between a rigid periodically wavy surface and a deformable half-space.
The deformable half-space is first considered to be elastic. The analytical solution of Boussinesq [2] is employed and adapted to periodically wavy surfaces [3,4]. The boundary element method is very efficient to solve contact problems because only the nominal contact area has to be meshed [5]. In addition, the number of elements in the mesh is considerably reduced when the periodical condition is taken into account since only the area over one reference period is needed to be considered. In order to validate the numerical method, the periodical pressure approach is first tested in the case of the contact between a sinusoidal rigid surface and an elastic smooth surface. The calculated contact areas and pressure distributions are compared to the analytical solutions and experimental results for one- and two-dimensional sinusoidal surfaces [1]. The numerical convergence has also been investigated in terms of number of elements and number of periods. It has been observed that the relative error between analytical and numerical contact forces decreases below 1%. Thus, the periodical pressure approach is fast, accurate, and efficient to solve contact problems of periodically wavy surfaces. Other periodical surfaces with paraboloidal, conical or pyramidal asperities are then analyzed and numerical solutions are compared to each other (Figure 2). These results have been published in the journal Meccanica [3].
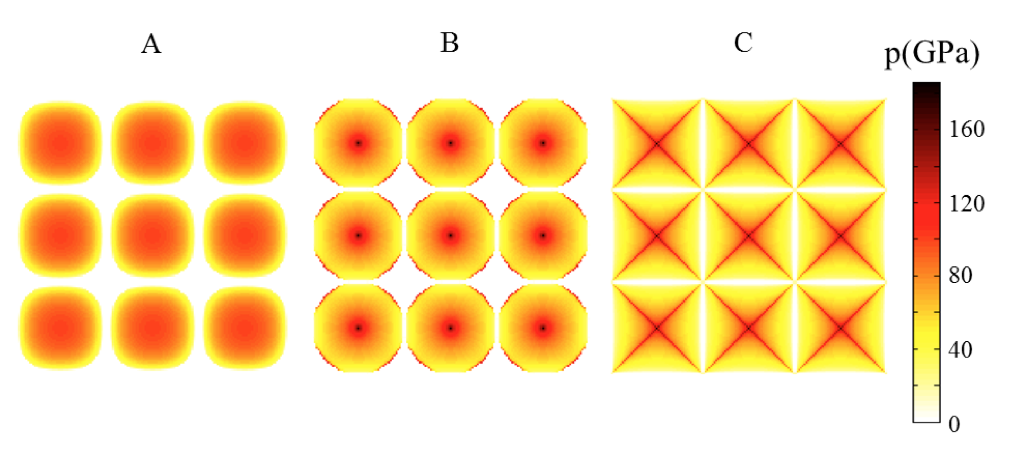
Figure 2: contact pressure distributions in the case of the contact between a periodical rigid surface containing paraboloidal (A), conical (B) and pyramidal (C) asperities, and an elastic half-space with a smooth surface.
It is seen that the asperity geometry has an important influence on the contact area and on the contact pressure distribution. Finally, different configurations of the rigid periodically wavy surface are considered where the position of the periods and the distance between asperities vary. It has been observed that these two factors have also a significant impact on the numerical results. These results have been published in the Journal of Mechanical Engineering Science [4].
Another having been done deals with the contact between a rigid half-space with a periodically wavy surface and a thermoelastic half-space with a smooth surface. The contact problem is studied by considering the assumptions quoted in the previous part and the heat flow between the contacting bodies is only permitted across the contact area, so the gap between the two solids, outside the contact area, acts like an isolating material. In this case, the vertical displacement of the thermoelastic surface is defined as the superposition of the elastic contribution of the contact pressure distribution, given by the solution of Boussinesq previously used, and the thermal displacement induced by the heat flow [6]. The vertical displacement, the contact area, the contact pressure distribution and the heat flow are taken to be periodic and the contact problem is still analyzed by focusing attention on only one period. The computational approach developed in the elastic context is used and tested in the case of one- and two-dimensional periodically wavy surfaces with sinusoidal, paraboloidal, conical and pyramidal asperities, and the resulting temperature distributions and heat flows are campared. It is first seen that the temperature distribution calculated for a one-dimensional sinusoidal surface is very close to its analytical solution. In addition, comparisons made reveal that the asperity geometry also affects the temperature distribution and the heat flow. It is also observed that the increasing of the temperature makes the contact area smaller. This is in agreement with the thermoelastic Hertzian solution [6].
Finally, the current work concerns the extension of the periodical pressure approach to the contact between a rigid periodically wavy surface and a viscoelastic smooth surface. The time-dependence makes this problem much more complex. The vertical displacement of the viscoelastic surface is given by the correspondence principle applied to its elastic expression obtained previously with the solution of Boussinesq. Numerical simulations are made, considering rigid sinusoidal surfaces with one- and two-dimensional profiles; the results obtained are compared with some relevant ones reported in the literature [1,7]. When a rigid wavy surface is sliding on a smooth viscoelastic surface, the pressure distribution on each contact area become asymmetric because of the loading condition at the leading edge and the unloading condition at the trailing edge of the contact area, also because of the viscoelastic behavior of the half-space.
References
[1] K.L. Johnson. Contact mechanics. Cambridge: Cambridge University Press, 1985.
[2] J. Boussinesq. Application des potentiels à l’étude de l’équilibre et du mouvement des solides élastiques. Paris: Gauthier-Villars, 1885.
[3] K. Houanoh, H.-P. Yin, Q.-C. He. A simple numerical approach for solving the frictionless contact problem of elastic wavy surfaces. Meccanica, 51: 463-473, 2016.
[4] K. Houanoh, H.-P. Yin, J. Cesbron, Q.-C. He. Influence of the in-plan distribution of asperities on the normal contact of periodically rough surfaces. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 230: 1382-1391, 2016.
[5] G. Dubois, J. Cesbron, H.P. Yin, F. Anfosso-Lédée. Numerical evaluation of tyre/road contact pressures using a multi-asperity approach. International Journal of Mechanical Sciences, 54: 84-94, 2012.
[6] Y.H. Jang, H. Cho, J.R. Barber. The thermoelastic Hertzian contact problem. International Journal of Solids and Structures, 46: 4073-4078, 2009.
[7] N. Menga, C. Putignano, G. Carbone, G. P. Demelio. The sliding contact of a rigid wavy surface with a viscoelastic half-space. Proceedings of the Royal Society A, 470: 20140392, 2014.
