Foams, made of a large number of gas bubbles (such that they are deformed by their neighbors) dispersed in a liquid, are commonly used in everyday life. Foams are desirable in many industrial processes such as in the mining industry to retrieve minerals from slurry, in enhanced oil recovery, or for the production of aerated building materials. The production of building materials is one of the more widespread examples of the production of so called aerated materials. For civil engineering applications, the addition of gas bubbles leads to various improvements of the final product, such as: the use of less raw material, a greater thermal or/and acoustic insulation as well as a reduced weight. More specifically, aerated complex materials are also used as templates for the production of metamaterials, showing particular acoustic properties due to their structure.
In all the industrial processes associated with the production of aerated materials the gas phase must be dispersed into a material having complex properties. For example, building materials such as concrete or plaster present a microstructure made of sand or gravel. The presence of such microstructure confers complex properties to the continuous phase (i.e more complex than for a simple liquid such as water): the material is often a complex fluid behaving in an intermediate way between simple liquids and elastic solids. Its microstructure is responsible for the material properties at the macroscopic scale (i.e. when deforming, or flowing). Among that class of materials, some behave like solids when the applied stress is lower than the critical stress (named yield stress), and like fluids otherwise.
In most industrial processes, complex aerated materials are obtained by batch processing: a yield stress fluid and a separately produced foam are mixed by mechanical means. Such methods provide little control over the stress state of the system and making high gas volume fraction difficult to obtain, with direct impact on the quality of the resulting material. Therefore, it raises the question of the production method of aerated yield-stress materials.
To produce dispersions of bubbles, or drops, of one fluid in another fluid the goal is always to break a large volume of the phase to disperse into smaller volumes (i.e. bubbles or droplets). Therefore, one must apply a stress that is sufficiently large to overcome interfacial stresses of the system due to surface tension. In this spirit, one method consists in injecting large bubbles, or a continuous stream of gas, into a pre-wetted porous medium constituted of interconnected channels. These geometries are complex and often exhibit rapid change in cross-sectional area which allows the formation of bubbles under various flow conditions and may not be satisfying to ensure a good control on bubble size (the dependency of preferential paths on the flow history, physicochemical characteristics of the medium through changes in wettability, interactions between multiple drops or bubbles may take place during the flow, leading to coalescences …).
In addition, as highlighted for Newtonian fluids in small scale geometries, the formation of bubbles or drops is always driven by capillary effects, therefore the presence of a yield stress, and possibly of solid regions where the stress is below the yield stress, may intrinsically hinder the capillary break-up. Finally, if the pre-wetting fluid had a yield stress, we can mention the role of dead volumes (where the stress is below the yield stress), it corresponds to approximately 10 % of the fluid in a porous medium made of glass beads. The presence of such dead regions increases the complexity of the flow and may also perturb the formation of bubbles or drops. This suggests the requirement for simpler geometry where the stress state is mostly known.
Microfluidics is a widely-used technology for performing diverse complex fluid manipulation, such as controlled droplet/bubbles transport or/and production, production of complex materials, or cell manipulation, as well as for performing chemical reaction, and ultimately for medical diagnosis and drug delivery. One of its main features is to allow the design of controlled geometry and the manufacturing of complex fluids at acceptable throughput with a highly accurate control on bubble size, and global flow rate. Recently, the production of monodisperse foams and emulsions as well as droplet manipulation and flow in microchannels has gained much interest, and knows a rapid expansion. Different simple geometries were develop to achieve this goal, the most popular being (i) T-junction, (ii) flow-focusing geometry, and (iii) step emulsification. Quite surprisingly, in spite of its popularity and the range of application that uses this technology, only a few literature reports of dispersions obtained in microfluidic systems using complex fluids or yield-stress fluids exist.
Recently, stereolithography techniques were developed and allow to fabricate millifluidic devices with micrometric precision. First, it presents the advantage to allow the freeform design of devices with circular cross sections, which reduces the complexity of the flow. Then, to work at the millimeter scale, thus minimizing the pressure drop associated with the flow of complex fluids which is generally large, and therefore possibly requires very high driving pressure that could damage micrometric geometries.
During his PhD thesis, Benoît Laborie investigate the formation of gas bubbles inside yield-stress fluids (YSF) using millifluidic T-junctions and flow-focusing devices (Fig. 1). Three main topics were studies : (i) bubble formation, (ii) the dynamics of the associated two phase flow, (iii) the characterization of steady regimes and the production of aerated yield-stress fluid foam.
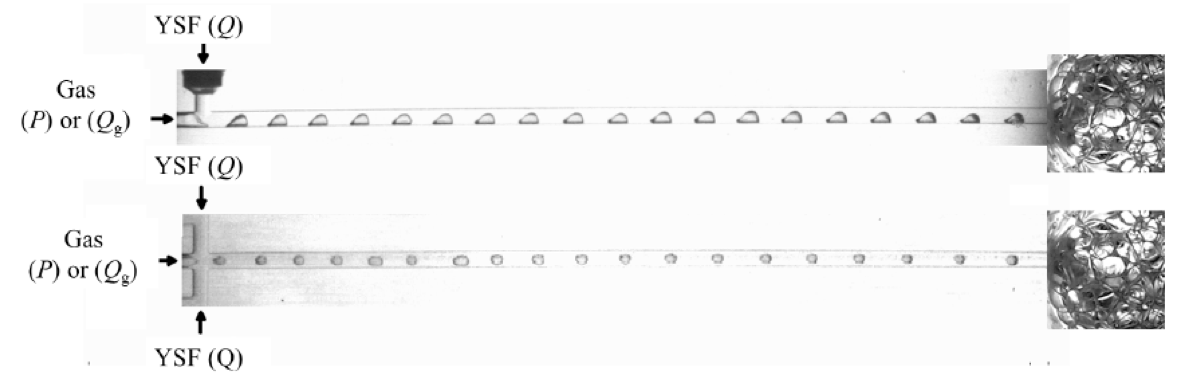
Figure 1: T-junction (top) and flow-focusing (bottom) devices with R = 1 mm and L = 10 filled with emulsion (E1). (a) the two phases meet inside the junction and the gas is dispersed inside the YSF. (b): bubbles are transported from the junction to the outlet of the device in a straight channel. (c) YSF foam forms at the outlet of the straight channel on a glass slide at atmospheric pressure for certain flow conditions and materials.
This work has shown that dispersing bubbles in simple yield-stress fluids (concentrated emulsions, and carbopol gels) is possible by taking advantage of the yield stress over the capillary stress, and due to the squeezing of the gas thread by the core of the yield-stress fluid flow at imposed flow rate [hal-01158022v1]. A limiting bubble frequency (1/ tminb) is identified (Fig 2, Left), the observed behavior is reminiscent of the geometrical operating regime in 2D flow-focusing devices for Newtonian fluids.
The different operating regimes have been investigated for imposed yield-stress fluid flow rate and the gas pressure [paper to be submitted]: three different regimes are reported, and compared to what is observed for Newtonian fluids. The validity domains of these regimes are detailed on a pressure/flow-rate diagram (Fig 2, Right). The critical pressure necessary to form the first bubble is measured and compared to the pressure associated with the yield-stress fluid flow at imposed flow rate. The bubble production is unsteady, which comes from the hydrodynamic feedback induced by the formation of each bubble on the gas flow rate. The regime eventually breaks down when all bubbles coalesce. This is due to the transfer between the liquid plugs separating each bubble and the thin film located on the channel wall. Thus, we study the deposition of yield-stress fluid on the wall of capillary tubes (i.e. the analogous of the Bretherton problem for Newtonian fluids) for steady and unsteady experiments as well as slip or no-slip conditions on channel wall. Indeed, this often occurs for yield-stress fluids flowing in confined geometries on smooth surfaces. The results with no-slip are well described by a classical scaling law (internal stresses balanced by capillary pressure gradient) [hal-JFM]. When there is wall slip, we show that there are three regimes that depend on the stress state of the system, and set the bubbles’ shape observed in unsteady regimes [hal-pof] (Figure 3). Finally, different regulation methods (pressure, pulsated flows) allow to obtain steady regimes. They are characterized (gas volume fraction, bubble formation time) and we show that they allow to obtain yield-stress fluid foams [paper to be submitted]. Thus, identifying pathways for potential steady-state controlled production of aerated yield-stress fluids at large scale.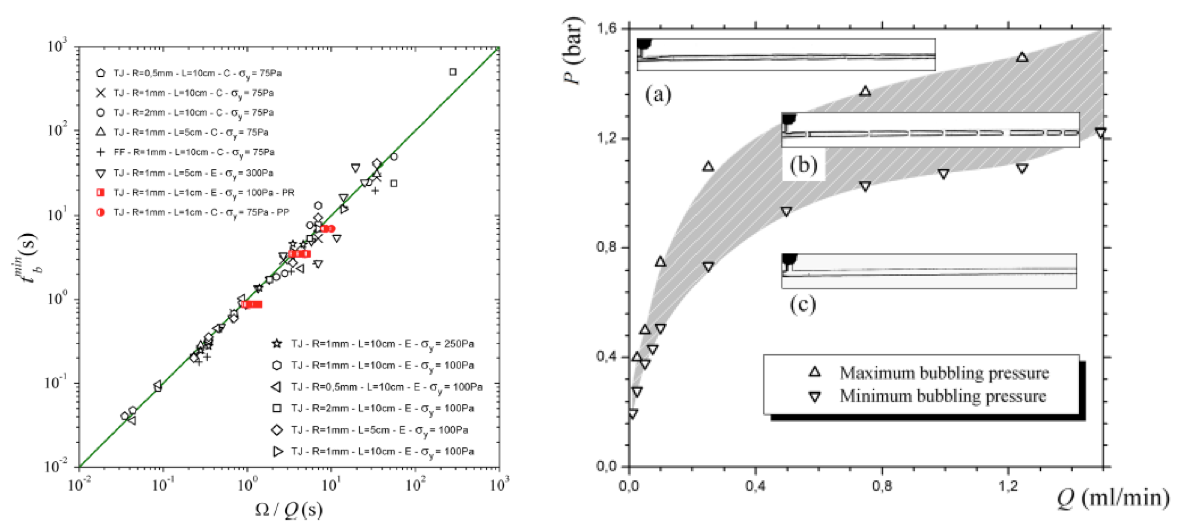
Figure 2: left– tminb as a function of Ω=Q for T-junction (TJ) and the flow-focusing (FF) geometries. The different symbols are detailed in the inset; (E) stands for emulsion, (C) for Carbopol. The red symbols correspond to different steady state bubble production. TJ, FF, PR, and PP, respectively, stand for T-junction, flow focusing, pressure regulation, and peristaltic pump. Right– Pressure/flow rate diagram for an emulsion (E3) in a T-junction (R = 1 mm and L = 10 cm). For a given flow rate the unsteady production of bubbles is observed between two critical (minimum and maximum) values of the applied pressure. (a) Above the maximum pressure, there is a co-flow of gas and YSF: no bubbles are produced.(c) Below the minimum bubbling pressure, there is a single phase flow: the gas meniscus moves backward and the device is only filled with YSF. (b) In between, there is an unsteady bubble production.
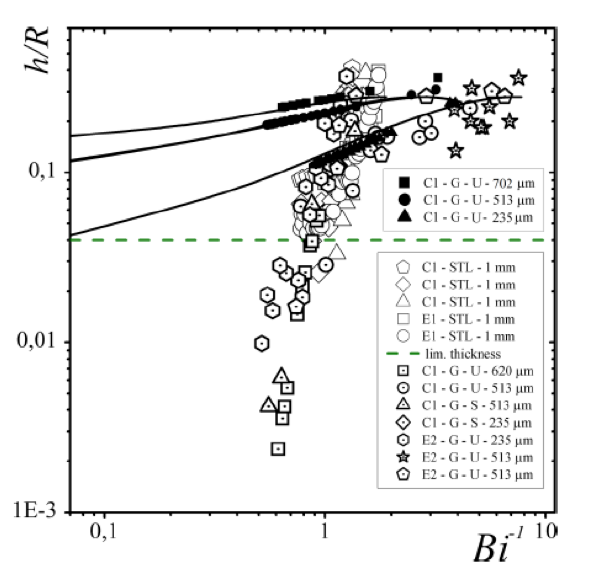
Figure 3: Normalized film thickness (h/R) as a function of the Bingham number for plug trains in STL channel (rough- empty symbols) and glass capillaries (G- dotted symbols) for different channel radii, materials, and steady (S) or unsteady (U) experiments in channel. The legend of the experiments is detailed in the inset. Filled symbols and plain lines correspond to deposition law for no-slip boundary conditions for with channels with (from top to bottom) R = 702, μm, 513 μm, 235 μm.
Publications:
Laborie, B., Rouyer, F., Angelescu, D. E. and Lorenceau, E., Yield-stress fluid deposition in circular channels, Journal of Fluids Mechanics, accepted.
Laborie, B., Rouyer, F., Angelescu, D. E. and Lorenceau, E. (2016) On the stability of the production of bubbles in yield-stress fluid using flow-focusing and T-junction devices, Phys. Fluids 28, 063103.
Laborie, B., Rouyer, F., Angelescu, D.E., Lorenceau, E. (2016) Yield-stress fluids foams: flow patterns and controlled production in T-junction and flow-focusing devices, Soft Matter, Volume 12, Issue 46, 2016, Pages 9355-9363
B. Laborie, F. Rouyer, D. E. Angelescu, and E. Lorenceau (2015) Bubble Formation in Yield Stress Fluids Using Flow-Focusing and T-Junction Devices, Physical Review Letters, 114(20), 204501 https://hal.archives-ouvertes.fr/hal-01158022/
